Crafting a null hypothesis for a chi-square test can seem a bit tricky, but it's an essential skill if you're diving into data analysis. You might have found yourself puzzled by the jargon or unsure where to start. Don't worry. You're not alone. In this guide, I'll walk you through what a null hypothesis is, how to write one for a chi-square test, and share some tips to ensure your hypothesis is on point.
What is a Null Hypothesis?
The null hypothesis is a fundamental concept in statistics, providing a baseline or default position that there is no effect or no difference. It's the skeptical perspective, the one that assumes the status quo. For example, if you're testing whether a coin is fair, the null hypothesis would state that the coin is unbiased, i.e., it has an equal chance of landing heads or tails.
Think of the null hypothesis as the "nothing changes" or "nothing to see here" stance. It's what you aim to test against to see if there‘s any evidence to support an alternative hypothesis, which proposes that there is some kind of effect or difference.
In statistical testing, we either reject the null hypothesis, suggesting that there is an effect, or fail to reject it, implying that we don't have enough evidence to say anything has changed. This doesn't prove the null hypothesis true; it simply indicates that the data doesn't provide strong enough evidence against it.
The Basics of the Chi-Square Test
The chi-square test is a versatile tool in statistics used to test relationships between categorical variables. There are two main types of chi-square tests: the chi-square test of independence and the chi-square test of goodness of fit.
- Chi-Square Test of Independence: This test assesses whether two categorical variables are independent. For example, you might want to know if there‘s a relationship between gender and preference for a new product.
- Chi-Square Test of Goodness of Fit: This test determines if a sample data matches a population with a specific distribution. It‘s useful when you want to see if observed data fits an expected distribution.
The test results in a statistic that helps you assess the likelihood that the observed differences arose by chance. If the probability is low enough, you may conclude that there is a statistically significant association or difference.
Writing Your Null Hypothesis for the Chi-Square Test
When writing a null hypothesis for a chi-square test, your goal is to assert that there is no association between the variables (for independence) or that the sample matches the expected distribution (for goodness of fit).
Here‘s a simple way to frame it:
H₀: There is no association between [Variable 1] and [Variable 2].
Or for a goodness of fit test:
H₀: The observed frequencies match the expected frequencies.
For example, if you‘re testing whether a dice is fair, your null hypothesis would be:
H₀: The dice shows a uniform distribution of outcomes (each number appears with equal frequency).
Common Mistakes and How to Avoid Them
Writing a null hypothesis might seem straightforward, but there are a few common pitfalls to watch out for:
- Being Too Vague: Make sure your hypothesis is specific enough to be testable. For instance, saying "there is no difference" without specifying the variables can lead to confusion.
- Mixing Up Null and Alternative Hypotheses: Remember, the null hypothesis always states that there is no effect or difference. The alternative hypothesis is where you state the expected effect or association.
- Using Biased Language: The null hypothesis should be neutral. Avoid language that implies a direction or preference.
By keeping these points in mind, you can avoid common errors and write a clear, concise null hypothesis.
Practical Example: Chi-Square Test for Independence
Let‘s say you‘re investigating whether there‘s a relationship between attending a workshop and passing a certification exam. You have data from a group of participants about whether they attended the workshop and whether they passed the exam.
Your null hypothesis would be:
H₀: Attendance at the workshop is independent of passing the certification exam.
Here, you‘re stating that attending the workshop doesn‘t affect the likelihood of passing the exam, which is exactly what the null hypothesis should do. Assert no relationship.
Practical Example: Chi-Square Test for Goodness of Fit
Consider a scenario where you‘re testing if a six-sided dice is fair. You roll the die 60 times and record the outcomes.
Your null hypothesis might look like this:
H₀: The outcomes of the dice rolls follow a uniform distribution (each number appears 10 times on average).
This hypothesis states that the dice is fair, as each outcome should appear roughly the same number of times if there‘s no bias.

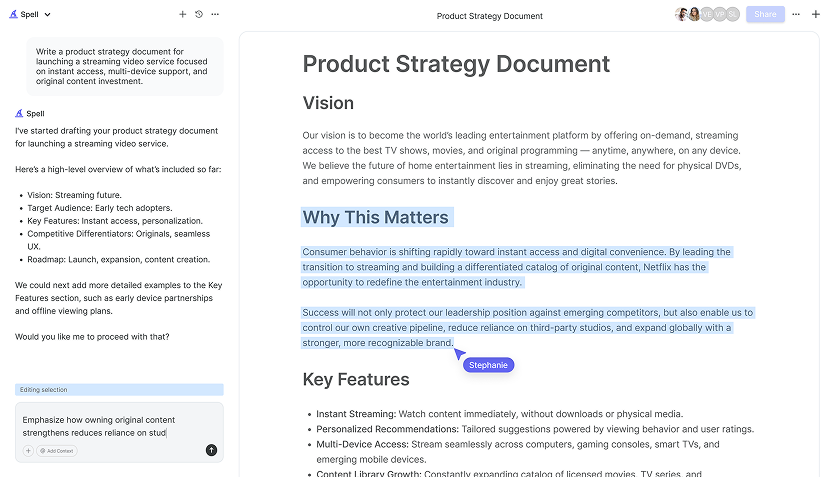
How Spell Can Assist in Writing Hypotheses
Writing hypotheses, especially for complex tests like chi-square, can be time-consuming and prone to errors. This is where Spell comes in handy. Spell helps streamline the process, allowing you to draft and refine your hypotheses quickly with AI assistance.
By using natural language prompts, you can instruct Spell to generate a first draft, which can save you time and help ensure your phrasing is accurate and clear. Plus, with its collaborative features, you can work with your team in real-time to fine-tune your documents without the hassle of alternating between different tools.
Tips for Testing Your Null Hypothesis
Once your null hypothesis is ready, the next step is testing it. Here are some tips to help you through the process:
- Choose the Right Test: Make sure the chi-square test you're using (independence vs. goodness of fit) matches your research question.
- Check Assumptions: Chi-square tests have assumptions, such as having a sufficiently large sample size and expected frequencies being 5 or more. Ensure your data meets these assumptions for accurate results.
- Interpret Results Correctly: Understand what rejecting or failing to reject the null hypothesis means in the context of your research. Rejection indicates evidence against the null, but failing to reject doesn‘t prove the null true.
Using Data to Support Your Hypothesis
Data is the backbone of hypothesis testing. When conducting a chi-square test, ensure your data is clean and accurately reflects the variables you‘re examining. Here are some pointers:
- Data Collection: Gather data systematically to avoid biases that might skew your results.
- Data Cleaning: Before running your test, clean your data to address any missing values or anomalies.
- Data Presentation: Present your data in a clear format, perhaps using tables or charts, to make interpretation easier.
With well-organized data, your hypothesis test will be more reliable, giving you confidence in your conclusions.
How to Refine Your Hypothesis with Feedback
Feedback is invaluable when it comes to refining your hypothesis. Whether it‘s peer reviews, supervisor input, or insights from software tools like Spell, constructive feedback can highlight areas for improvement.
Consider revisiting your hypothesis after getting feedback. Ask yourself:
- Is my hypothesis clear and concise?
- Does it align with the research question?
- Have I avoided common pitfalls like bias or vagueness?
Using feedback effectively can lead to a more robust and testable hypothesis, ultimately strengthening your research.
Final Thoughts
Crafting a null hypothesis for a chi-square test doesn't have to be daunting. With the right approach and tools, you can write clear, testable hypotheses that enhance your research. Tools like Spell can make the process faster and more efficient by providing AI-generated drafts and real-time collaboration features. Remember, practice makes perfect, so keep refining your skills as you go






