How to Write a Proof

Coming up with a solid mathematical proof can feel as intricate as weaving a tapestry. Each thread must intertwine logically with the others, creating a seamless pattern of reasoning. In this post, we'll unravel the steps you need to create compelling proofs that hold up under scrutiny. Whether you're tackling homework problems or presenting your findings to peers, understanding how to write a proof is a skill that can open doors in mathematics and beyond.

What Exactly Is a Proof?

Before we get into the nuts and bolts of proof-writing, it’s helpful to know what a proof actually is. In the world of mathematics, a proof is a logical argument that establishes the truth of a statement. It's not just about showing that something is true but demonstrating why it's true through a series of logical steps.

Think of a proof as a story where each sentence builds upon the last. Like any good story, a proof must start somewhere familiar (known facts) and lead the reader to a new understanding (the conclusion). For example, if you were proving the Pythagorean theorem, you'd start with the definitions and properties of triangles and move step-by-step to show that a² + b² = c².

Choosing the Right Type of Proof

Not all proofs are created equal; different problems require different approaches. Here are a few common types of proofs you might encounter:

• Direct Proof: This is the straight-line approach where you start with the given information and use logical steps to arrive at the conclusion. It‚Äôs like following a recipe. Add ingredients one by one, and voil√†, you have your dish!
• Proof by Contradiction: Assume the opposite of what you want to prove is true. Then, show that this assumption leads to a contradiction. It‚Äôs like saying, ‚ÄúIf this were true, then pigs really could fly,‚Äù which highlights the absurdity of the assumption.
• Proof by Induction: This method is particularly useful for proving statements about integers. You demonstrate the statement is true for an initial case and then prove that if it's true for one case, it's true for the next. Think of it as setting up dominoes. Once the first falls, the rest follow.

Knowing which type of proof to use can make the process much smoother. For instance, if you’re working with an infinite series, induction might be your best bet. On the other hand, if you're tackling a problem with a clear logical path, a direct proof could be the way to go.

Starting with Definitions and Known Facts

Every proof begins with a solid foundation. That means starting with definitions and known facts. These are the bedrock upon which your entire argument will rest. For example, if you're dealing with geometric shapes, you'll want to start by defining those shapes and any relevant properties.

Consider proving that the sum of the angles in a triangle is 180 degrees. You'd begin with the definitions of a triangle and angle, then move to known theorems, such as the supplementary angles theorem. This groundwork sets you up for success, as each step you take will build logically from these initial truths.

Here's a tip. Keep a glossary of definitions and theorems handy. Whether it’s in a notebook or a digital document, having quick access to these can save you time and ensure accuracy in your proofs.

Breaking Down the Problem

Once you've got your definitions and facts in place, it's time to dissect the problem. This involves understanding what you're trying to prove and breaking it down into manageable parts. Ask yourself. What are the components of the statement? What needs to be shown?

Let’s say you’re tasked with proving that the square root of 2 is irrational. Break it down. You need to show that there are no two integers, a and b, such that (a/b)² = 2. Each part of the proof will tackle a piece of this puzzle. By isolating the elements, you make the task less daunting and more approachable.

Creating the Logical Flow

Now comes the fun part. Building your argument. This is where you get to play with logic and create a flow that leads from your starting point to the conclusion. A well-structured proof will guide the reader naturally from one idea to the next.

Think of your proof as a roadmap. Each step should follow logically from the last, like directions on a journey. If you're using a direct proof, you might start with your given and use it to derive new pieces of information until you reach your destination. For a proof by contradiction, you’ll take a detour, assuming the opposite and showing how it leads to a dead end.

For example, if you're proving that the sum of any two even numbers is even, you might start with two integers, say 2m and 2n (since any even number can be expressed as 2 times an integer). Then, show that their sum, 2m + 2n, is also divisible by 2, leading to the conclusion.

Using Clear and Concise Language

Clarity is crucial in a proof. You want your reader to follow your logic without stumbling over ambiguous language or convoluted explanations. Each step should be expressed clearly and concisely, leaving no room for doubt.

Consider this. If your proof were a recipe, each instruction should be easy to follow. Instead of saying “Mix ingredients until they form a homogeneous mixture,” opt for “Stir the flour and sugar together until blended.” Keep it simple and direct.

When writing, avoid jargon that might confuse your audience. Use straightforward language and clear notation. If you need to introduce a new term or symbol, define it immediately. This way, you're not just proving your point; you're teaching the reader along the way.

Reviewing and Refining Your Proof

Once you've constructed your proof, it’s time to put on your editor's hat. Review your work critically, checking for logical consistency, clarity, and correctness. This stage is crucial for catching any errors or weaknesses in your argument.

Ask yourself:

• Does each step follow logically from the last?
• Have I used clear and concise language?
• Are all definitions and assumptions stated?

Consider having a peer or mentor review your proof as well. A fresh set of eyes can catch mistakes you might have missed. And remember, even the best mathematicians refine their work multiple times before reaching a final draft.

Documenting the Proof in a Polished Way

Finally, present your proof in a polished format. This involves not only the logical content but the visual presentation as well. A neatly formatted proof is easier to read and more convincing.

Use headings, bullet points, and numbered steps to organize your proof. This structure helps guide the reader through your argument, making complex ideas more digestible. For example:

1. Assume two integers, a and b, such that (a/b)^2 = 2.
2. Express a and b in their simplest form, meaning they have no common factors.
3. Show that both a^2 and b^2 must be even, leading to a contradiction.
4. Conclude that no such integers exist, proving the square root of 2 is irrational.

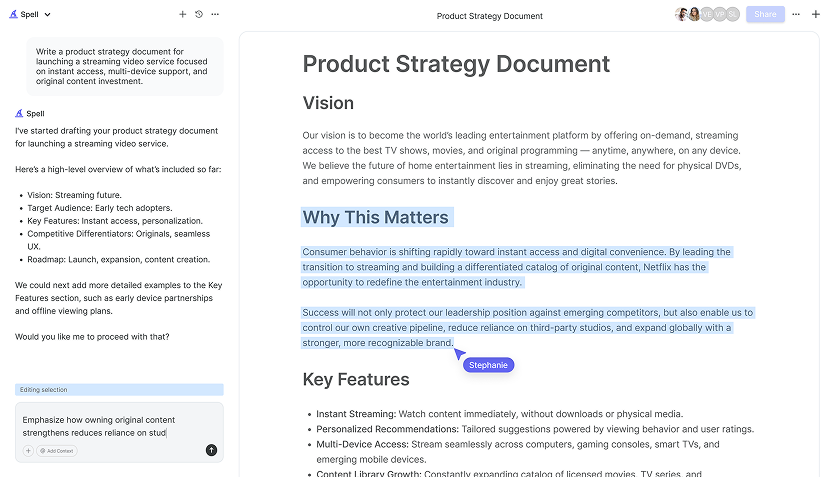
Consider using tools like Spell to draft and refine your proofs. With AI-powered editing and collaboration features, Spell can help you focus on crafting a compelling argument without getting bogged down in formatting or syntax.

Practicing Proof-Writing Regularly

Like any skill, proof-writing improves with practice. Regularly challenging yourself with new problems will sharpen your logic and reasoning abilities. Start with simpler proofs and gradually work your way up to more complex ones.

Create a routine where you dedicate time to writing proofs. This doesn't mean hours on end. Just a consistent, manageable amount of time that fits your schedule. Over time, you'll notice improvements in your ability to think critically and articulate your thoughts clearly.

And remember, there's no shame in revisiting basic concepts. Sometimes, a refresher on foundational topics can provide new insights and strengthen your overall proof-writing skills.

Final Thoughts

Writing a mathematical proof is both an art and a science. It requires a balance of creative thinking and logical precision. By understanding the different types of proofs, building on solid definitions, and practicing regularly, you can develop this skill into a powerful tool for problem-solving. If you're looking to streamline your writing process, consider using Spell to draft and edit your proofs efficiently. With practice and the right tools, crafting a convincing proof becomes less daunting and more of an engaging intellectual exercise.